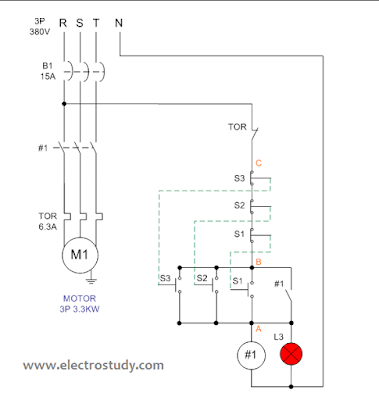
Wiring diagram 3 phase motor 3.3 kW with three unit of BSH 222 switch

We will use three unit of BSH 222 switch for control a motor glue pump. The glue must distribute to three different location, such us Line1, Line2 and Line3. Each switch store in each Line location.

Wiring diagram 3 phase motor 3.3 kW with three unit of BSH 222 switch

Electric parts needed for the wiring 3 Phase motor 3.3 kW with three unit of BSH 222 switch above:

• B1 = MCB 15A 3 phase
• M1 = Motor 3.3kW 380V 3Phase
• #1 = Magnetic contactor 220VAC
• TOR = Thermal overload relay 6.3A
• S1, S2, S3 = Push button switch type BSH 222
• L3 = Pilot lamp 220VAC

Wiring connection of BSH 222 switch

BHS 222 switch has an two contacts switch, NO (Normally Open for ON button) Contact and NC (Normally Close for OFF button) contact. In wiring 3 Phase motor 3.3 kW with three unit of BSH 222 switch, we use to series connection the NC contact and to parallel connection the NO contact.

Read more »»

BSH 222 Switch

BSH 222 is a Type of Push Button Switch

Kasuga BSH 222 is a type of push button switch, which has an ON button and an OFF button in one switch. ON button BSH 222 marked with black color, position above OFF button. OFF button BSH 222 marked with red color, position below ON button.

BSH 222

PTM and PTB

ON button in a BSH 222 switch is type of PTM (push to make) non latching. OFF button in a BSH 222 switch is type of PTB (push to brake) non latching. Picture below is a symbol of BHS 222 switch.

Contact Capacity

Electric voltage and current capacity of the contact point BSH 222:
250 V max 5 A
500 V max 1 A.

Purpose

BSH 222 switch usually used for control (start and stop) small electric motor. For some case, one motor is controlled by many BSH 222 switch. One unit BSH 222 and other unit of them, are placed in different location, use for control a motor, such us motor glue pump who will distribute the glue for each location.

Read more »»

Wiring diagram 3 phase motor 2.2 kW with stop series connection

In most industrial system control machine, there's a start switch and there' re a lot of stop switch. Start switch location is on the panel operator. Stop switches location are on the control box, in each unit of the machine. Stop switch connection in wiring diagram are series connections.

Wiring diagram 3 Phase motor 2.2 kW with stop series connection

Electric parts needed for the wiring 3 phase motor 2.2 kW above::

1. B1 = MCB 10A 3 phase
2. M1 = Motor 2.2kW 380V 3Phase
3. #1 = Magnetic contactor 220VAC
4. TOR = Thermal Overload Relay 4.2A
5. S1, S2, S3 = Push Button Switch (PTB non latching - stop switch)
6. S4 = Push Button Switch (PTM non latching - start switch)
7. L3 = Pilot lamp 220VAC

Read more »»

Wiring diagram single motor with Start - Stop switch

Basic control motor, to get start or stop the motor, use a push button switch as a trigger a motor. Push To Make / PTM switch use to start the motor and Push To Brake / PTB switch use to stop the motor.

Wiring diagram single motor with Start - Stop switch

Electric parts needed for the wiring above:

1. B1 = MCB 5A 3 phase
2. M1 = Motor 1.5kW 380V 3Phase
3. #1 = Magnetic contactor 220VAC
4. TOR = Thermal Overload Relay 2.8A
5. S1 = Push Button Switch (PTB non latching - Stop switch)
6. S2 = Push Button Switch (PTM non latching - Start switch)
7. L3 = Pilot lamp 220VAC

Read more »»

Wiring diagram single motor with selector switch

Basic control motor, to get start or stop the motor, only use a selector switch as a trigger a motor.

Wiring diagram single motor with selector switch

Electric parts needed for the wiring above:

1. B1 = MCB 5A 3 phase
2. M1 = Motor 0.75kW 380V 3Phase
3. #1 = Magnetic contactor 220VAC
4. TOR = Thermal Overload Relay 1.4A
5. S1 = Selector Switch
6. L3 = Pilot lamp 220VAC

Read more »»

Hexadecimal number system 1 - 100

Hexadecimal number system is numeral system with a base of 16. Represents numeric values using sixteen symbols, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E and F.

Table below is hexadecimal number from 1 to 64, equivalent of 1 to 100 in decimal number.

Hexadecimal	Decimal	Hexadecimal	Decimal
1	1	33	51
2	2	34	52
3	3	35	53
4	4	36	54
5	5	37	55
6	6	38	56
7	7	39	57
8	8	3A	58
9	9	3B	59
A	10	3C	60
B	11	3D	61
C	12	3E	62
D	13	3F	63
E	14	40	64
F	15	41	65
10	16	42	66
11	17	43	67
12	18	44	68
13	19	45	69
14	20	46	70
15	21	47	71
16	22	48	72
17	23	49	73
18	24	4A	74
19	25	4B	75
1A	26	4C	76
1B	27	4D	77
1C	28	4E	78
1D	29	4F	79
1E	30	50	80
1F	31	51	81
20	32	52	82
21	33	53	83
22	34	54	84
23	35	55	85
24	36	56	86
25	37	57	87
26	38	58	88
27	39	59	89
28	40	5A	90
29	41	5B	91
2A	42	5C	92
2B	43	5D	93
2C	44	5E	94
2D	45	5F	95
2E	46	60	96
2F	47	61	97
30	48	62	98
31	49	63	99
32	50	64	100

Read more »»

Octal number system 1 - 100

Octal number system is numeral system with a base of 8. Represents numeric values using eight symbols, 0, 1, 2, 3, 4, 5, 6 and 7. There is no 8 or 9 in octal number system.

Table below is octal number from 1 to 144, equivalent of 1 to 100 in decimal number.

Octal	Decimal	Octal	Decimal
1	1	63	51
2	2	64	52
3	3	65	53
4	4	66	54
5	5	67	55
6	6	70	56
7	7	71	57
10	8	72	58
11	9	73	59
12	10	74	60
13	11	75	61
14	12	76	62
15	13	77	63
16	14	100	64
17	15	101	65
20	16	102	66
21	17	103	67
22	18	104	68
23	19	105	69
24	20	106	70
25	21	107	71
26	22	110	72
27	23	111	73
30	24	112	74
31	25	113	75
32	26	114	76
33	27	115	77
34	28	116	78
35	29	117	79
36	30	120	80
37	31	121	81
40	32	122	82
41	33	123	83
42	34	124	84
43	35	125	85
44	36	126	86
45	37	127	87
46	38	130	88
47	39	131	89
50	40	132	90
51	41	133	91
52	42	134	92
53	43	135	93
54	44	136	94
55	45	137	95
56	46	140	96
57	47	141	97
60	48	142	98
61	49	143	99
62	50	144	100

Read more »»

Binary number system 1 - 100

Binary number system is numeral system with a base of 2. Represents numeric values using two symbols, 0 and 1. There is no 2,3,4,5,6,7,8 or 9 in binary number system.

Table below is binary number from 1 to 1100100, equivalent of 1 to 100 in decimal number.

Binary	Decimal	Binary	Decimal
1	1	110011	51
10	2	110100	52
11	3	110101	53
100	4	110110	54
101	5	110111	55
110	6	111000	56
111	7	111001	57
1000	8	111010	58
1001	9	111011	59
1010	10	111100	60
1011	11	111101	61
1100	12	111110	62
1101	13	111111	63
1110	14	1000000	64
1111	15	1000001	65
10000	16	1000010	66
10001	17	1000011	67
10010	18	1000100	68
10011	19	1000101	69
10100	20	1000110	70
10101	21	1000111	71
10110	22	1001000	72
10111	23	1001001	73
11000	24	1001010	74
11001	25	1001011	75
11010	26	1001100	76
11011	27	1001101	77
11100	28	1001110	78
11101	29	1001111	79
11110	30	1010000	80
11111	31	1010001	81
100000	32	1010010	82
100001	33	1010011	83
100010	34	1010100	84
100011	35	1010101	85
100100	36	1010110	86
100101	37	1010111	87
100110	38	1011000	88
100111	39	1011001	89
101000	40	1011010	90
101001	41	1011011	91
101010	42	1011100	92
101011	43	1011101	93
101100	44	1011110	94
101101	45	1011111	95
101110	46	1100000	96
101111	47	1100001	97
110000	48	1100010	98
110001	49	1100011	99
110010	50	1100100	100

Read more »»

Hexadecimal numbers to octal numbers

Convert hexadecimal numbers to octal numbers
1. F4
2. ADE
3. 8C1F

Completion:
1. F4 ₍₁₆₎ = ? ₍₈₎
* First, convert hexadecimal numbers to decimal numbers. Then, convert decimal numbers to octal numbers.

hexadecimal to decimal
F4 = 4x16⁰ + Fx16¹
F4 = 4x16⁰ + 15x16¹
F4 = 4 + 240
F4 ₍₁₆₎ = 244 ₍₁₀₎

decimal to octal
244 / 8 = 30, remains 4
30 / 8 = 3, remains 6
3 / 8 = 0, remains 3
244 ₍₁₀₎ = 364 ₍₈₎

F4 hexadecimal number equal to 364 octal number
F4 ₍₁₆₎ = 364 ₍₈₎

2. ADE ₍₁₆₎ = ? ₍₈₎
hexadecimal to decimal
ADE = Ex16⁰ + Dx16¹ + Ax16²
ADE = 14x16⁰ + 13x16¹ + 10x16²
ADE = 14 + 208 + 2560
ADE ₍₁₆₎ = 2782 ₍₁₀₎

decimal to octal
2782 / 8 = 347, remains 6
347 / 8 = 43, remains 3
43 / 8 = 5, remains 3
5 / 8 = 0, remains 5
3501 ₍₁₀₎ = 5336 ₍₈₎

ADE hexadecimal number equal to 5336 octal number
ADE ₍₁₆₎ = 5336 ₍₈₎

3. 8C1F ₍₁₆₎ = ? ₍₈₎
hexadecimal to decimal
8C1F = Fx16⁰ + 1x16¹ + Cx16² + 8x16³
8C1F = 15x16⁰ + 1x16¹ + 12x16² + 8x16³
8C1F = 15 + 16 + 3072 + 32768
8C1F ₍₁₆₎ = 35871 ₍₁₀₎

decimal to octal
35871 / 8 = 4483, remains 7
4483 / 8 = 560, remains 3
560 / 8 = 70, remains 0
70 / 8 = 8, remains 6
8 / 8 = 1, remains 0
1 / 8 = 0, remains 1
605025 ₍₁₀₎ = 106037 ₍₈₎

8C1F hexadecimal number equal to 106037 octal number
8C1F ₍₁₆₎ = 106037 ₍₈₎

Read more »»

Hexadecimal numbers to binary numbers

Convert hexadecimal numbers to binary numbers
1. 2B
2. DAD
3. FE01

Completion:
1. 2B ₍₁₆₎ = ? ₍₂₎
* First, convert hexadecimal numbers to decimal numbers. Then, convert decimal numbers to binary numbers.

hexadecimal to decimal
2B = Bx16⁰ + 2x16¹
2B = 11x16⁰ + 2x16¹
2B = 11 + 32
2B ₍₁₆₎ = 43 ₍₁₀₎

decimal to binary
43 / 2 = 21, remains 1
21 / 2 = 10, remains 1
10 / 2 = 5, remains 0
5 / 2 = 2, remains 1
2 / 2 = 1, remains 0
1 / 2 = 0, remains 1
43 ₍₁₀₎ = 101011 ₍₂₎

2B hexadecimal number equal to 101011 binary number
2B ₍₁₆₎ = 101011 ₍₂₎

2. DAD ₍₁₆₎ = ? ₍₂₎
hexadecimal to decimal
DAD = Dx16⁰ + Ax16¹ + Ax16²
DAD = 13x16⁰ + 10x16¹ + 13x16²
DAD = 13 + 160 + 3328
DAD ₍₁₆₎ = 3501 ₍₁₀₎

decimal to binary
3501 / 2 = 1750, remains 1
1750 / 2 = 875, remains 0
875 / 2 = 437, remains 1
437 / 2 = 218, remains 1
218 / 2 = 109, remains 0
109 / 2 = 54, remains 1
54 / 2 = 27, remains 0
27 / 2 = 13, remains 1
13 / 2 = 6, remains 1
6 / 2 = 3, remains 0
3 / 2 = 1, remains 1
1 / 2 = 0, remains 1
3501 ₍₁₀₎ = 110110101101 ₍₂₎

DAD hexadecimal number equal to 110110101101 binary number
DAD ₍₁₆₎ = 110110101101 ₍₂₎

3. FE01 ₍₁₆₎ = ? ₍₂₎
hexadecimal to decimal
FE01 = 1x16⁰ + 0x16¹ + Ex16² + Fx16³
FE01 = 1x16⁰ + 0x16¹ + 14x16² + 15x16³
FE01 = 1 + 0 + 3584 + 61440
FE01 ₍₁₆₎ = 65025 ₍₁₀₎

decimal to binary
65025 / 2 = 32512, remains 1
32512 / 2 = 16256, remains 0
16256 / 2 = 8128, remains 0
8128 / 2 = 4064, remains 0
4064 / 2 = 2032, remains 0
2032 / 2 = 1016, remains 0
1016 / 2 = 508, remains 0
508 / 2 = 254, remains 0
254 / 2 = 127, remains 0
127 / 2 = 63, remains 1
63 / 2 = 31, remains 1
31 / 2 = 15, remains 1
15 / 2 = 7, remains 1
7 / 2 = 3, remains 1
3 / 2 = 1, remains 1
1 / 2 = 0, remains 1
605025 ₍₁₀₎ = 1111111000000001 ₍₂₎

FE01 hexadecimal number equal to 1111111000000001 binary number
FE01 ₍₁₆₎ = 1111111000000001 ₍₂₎

Read more »»

Octal numbers to hexadecimal numbers

Convert octal numbers to hexadecimal numbers
1. 73
2. 305
3. 5431

Completion:
1. 73 ₍₈₎ = ? ₍₁₆₎
* First, convert octal numbers to decimal numbers. Then, convert decimal numbers to hexadecimal numbers.

octal to decimal
73 = 3x8⁰ + 7x8¹
73 = 3 + 56
73 ₍₈₎ = 59 ₍₁₀₎

decimal to hexadecimal
59 / 16 = 3, remains 11 or B
3 / 16 = 0, remains 3
59 ₍₁₀₎ = 3B ₍₁₆₎

73 octal number equal to 3B hexadecimal number
73 ₍₈₎ = 3B ₍₁₆₎

2. 305 ₍₈₎ = ? ₍₁₆₎
octal to decimal
305 = 5x8⁰ + 0x8¹ + 3x8²
305 = 5 + 0 + 192
305 ₍₈₎ = 197 ₍₁₀₎

decimal to hexadecimal
197 / 16 = 12, remains 5
12 / 16 = 0, remains 12 or C
197 ₍₁₀₎ = C5 ₍₁₆₎

305 octal number equal to C5 hexadecimal number
305 ₍₈₎ = C5 ₍₁₆₎

3. 5431 ₍₈₎ = ? ₍₁₆₎
octal to decimal
5431 = 1x8⁰ + 3x8¹ + 4x8² + 5x8³
5431 = 1 + 24 + 256 + 2560
5431 ₍₈₎ = 2841 ₍₁₀₎

decimal to hexadecimal
2841 / 16 = 177, remains 9
177 / 16 = 11, remains 1
11 / 16 = 0, remains 11 or B
2841 ₍₁₀₎ = B19 ₍₁₆₎

5431 octal number equal to B19 hexadecimal number
5431 ₍₈₎ = B19 ₍₁₆₎

Read more »»

Octal numbers to binary numbers

Convert octal numbers to binary numbers
1. 45
2. 700
3. 2021

Completion:
1. 45 ₍₈₎ = ? ₍₂₎
* First, convert octal numbers to decimal numbers. Then, convert decimal numbers to binary numbers.

octal to decimal
45 = 5x8⁰ + 4x8¹
45 = 5 + 32
45 ₍₈₎ = 37 ₍₁₀₎

decimal to binary
37 / 2 = 18, remains 1
18 / 2 = 9, remains 0
9 / 2 = 4, remains 1
4 / 2 = 2, remains 0
2 / 2 = 1, remains 0
1 / 2 = 0, remains 1
37 ₍₁₀₎ = 100101 ₍₂₎

45 octal number equal to 100101 binary number
45 ₍₈₎ = 100101 ₍₂₎

2. 700 ₍₈₎ = ? ₍₂₎
octal to decimal
700 = 0x8⁰ + 0x8¹ + 7x8²
700 = 0 + 0 + 448
700 ₍₈₎ = 448 ₍₁₀₎

decimal to binary
448 / 2 = 224, remains 0
224 / 2 = 112, remains 0
112 / 2 = 56, remains 0
56 / 2 = 28, remains 0
28 / 2 = 14, remains 0
14 / 2 = 7, remains 0
7 / 2 = 3, remains 1
3 / 2 = 1, remains 1
1 / 2 = 0, remains 1
448 ₍₁₀₎ = 111000000 ₍₂₎

700 octal number equal to 111000000 binary number
700 ₍₈₎ = 111000000 ₍₂₎

3. 2021 ₍₈₎ = ? ₍₂₎
octal to decimal
2021 = 1x8⁰ + 2x8¹ + 0x8² + 2x8³
2021 = 1 + 16 + 0 + 1024
2021 ₍₈₎ = 1041 ₍₁₀₎

decimal to binary
1041 / 2 = 520, remains 1
520 / 2 = 260, remains 0
260 / 2 = 130, remains 0
130 / 2 = 65, remains 0
65 / 2 = 32, remains 1
32 / 2 = 16, remains 0
16 / 2 = 8, remains 0
8 / 2 = 4, remains 0
4 / 2 = 2, remains 0
2 / 2 = 1, remains 0
1 / 2 = 0, remains 1
1041 ₍₁₀₎ = 10000010001 ₍₂₎

2021 octal number equal to 10000010001 binary number
2021 ₍₈₎ = 10000010001 ₍₂₎

Read more »»

Binary numbers to hexadecimal numbers

Convert binary numbers to hexadecimal numbers
1. 11111
2. 1101110
3. 1110101010

Completion:
1. 11111 ₍₂₎ = ? ₍₁₆₎
* First, convert binary numbers to decimal numbers. Then, convert decimal numbers to hexadecimal numbers.

binary to decimal
11111 = 1x2⁰ + 1x2¹ + 1x2² + 1x2³ + 1x2⁴
11111 = 1 + 2 + 4 + 8 + 16
11111 ₍₂₎ = 31 ₍₁₀₎

decimal to hexadecimal
31 / 16 = 1, remains 15 or F
1 / 16 = 0, remains 1
31 ₍₁₀₎ = 1F ₍₁₆₎

11111 binary number equal to 1F hexadecimal number
11111 ₍₂₎ = 1F ₍₁₆₎

2. 1101110 ₍₂₎ = ? ₍₁₆₎
binary to decimal
1101110 = 0x2⁰ + 1x2¹ + 1x2² + 1x2³ + 0x2⁴ + 1x2⁵ + 1x2⁶
1101110 = 0 + 2 + 4 + 8 + 0 + 32 + 64
1101110 ₍₂₎ = 110 ₍₁₀₎

decimal to hexadecimal
110 / 16 = 6, remains 14 or E
6 / 16 = 0, remains 6
79 ₍₁₀₎ = 6E ₍₁₆₎

1101110 binary number equal to 6E hexadecimal number
1101110 ₍₂₎ = 6E ₍₁₆₎

3. 1110101010 ₍₂₎ = ? ₍₁₆₎
binary to decimal
1110101010 = 0x2⁰ + 1x2¹ + 0x2² + 1x2³ + 0x2⁴ + 1x2⁵ + 0x2⁶ + 1x2⁷ + 1x2⁸ + 1x2⁹
1110101010 = 0 + 2 + 0 + 8 + 0 + 32 + 0 + 128 + 256 + 512
1110101010 ₍₂₎ = 938 ₍₁₀₎

decimal to hexadecimal
938 / 16 = 58, remains 10 or A
58 / 16 = 3, remains 10 or A
3 / 16 = 0, remains 3
938 ₍₁₀₎ = 3AA ₍₁₆₎

1110101010 binary number equal to 3AA hexadecimal number
1110101010 ₍₂₎ = 3AA ₍₁₆₎

Read more »»

Binary numbers to octal numbers

Convert binary numbers to octal numbers
1. 11101
2. 1001111
3. 1010101010

Completion:
1. 11101 ₍₂₎ = ? ₍₈₎
* First, convert binary numbers to decimal numbers. Then, convert decimal numbers to octal numbers.

binary to decimal
11101 = 1x2⁰ + 0x2¹ + 1x2² + 1x2³ + 1x2⁴
11101 = 1 + 0 + 4 + 8 + 16
11101 ₍₂₎ = 29 ₍₁₀₎

decimal to octal
29 / 8 = 3, remains 5
3 / 8 = 0, remains 3
29 ₍₁₀₎ = 35 ₍₈₎

11101 binary number equal to 35 octal number
11101 ₍₂₎ = 35 ₍₈₎

2. 1001111 ₍₂₎ = ? ₍₈₎
binary to decimal
1001111 = 1x2⁰ + 1x2¹ + 1x2² + 1x2³ + 0x2⁴ + 0x2⁵ + 1x2⁶
1001111 = 1 + 2 + 4 + 8 + 0 + 0 + 64
1001111 ₍₂₎ = 79 ₍₁₀₎

decimal to octal
79 / 8 = 9, remains 7
9 / 8 = 1, remains 1
1 / 8 = 0, remains 1
79 ₍₁₀₎ = 117 ₍₈₎

1001111 binary number equal to 117 octal number
1001111 ₍₂₎ = 117 ₍₈₎

3. 1010101010 ₍₂₎ = ? ₍₈₎
binary to decimal
1010101010 = 0x2⁰ + 1x2¹ + 0x2² + 1x2³ + 0x2⁴ + 1x2⁵ + 0x2⁶ + 1x2⁷ + 0x2⁸ + 1x2⁹
1010101010 = 0 + 2 + 0 + 8 + 0 + 32 + 0 + 128 + 0 + 512
1010101010 ₍₂₎ = 682 ₍₁₀₎

decimal to octal
682 / 8 = 85, remains 2
85 / 8 = 10, remains 5
10 / 8 = 1, remains 2
1 / 8 = 0, remains 1
682 ₍₁₀₎ = 1252 ₍₈₎

1010101010 binary number equal to 1252 octal number
1010101010 ₍₂₎ = 1252 ₍₈₎

Read more »»

Decimal numbers to hexadecimal numbers

Convert decimal numbers to hexadecimal numbers
1. 128
2. 2015
3. 300000

Completion:
1. 128 ₍₁₀₎ = ? ₍₁₆₎
→ 128 / 16 = 8, remains 0
→ 8 / 16 = 0, remains 8
* Finish when meet zero (0) and then write remains numbers, from bottom to top.
128 decimal number equal to 80 hexadecimal number
128 ₍₁₀₎ = 80 ₍₁₆₎

2. 2015 ₍₁₀₎ = ? ₍₁₆₎
2015 / 16 = 125, remains 15 or F
125 / 16 = 7, remains 13 or D
7 / 16 = 0, remains 7
2015 decimal number equal to 7DF hexadecimal number
2015 ₍₁₀₎ = 7DF ₍₁₆₎

3. 300000 ₍₁₀₎ = ? ₍₁₆₎
300000 / 16 = 18750, remains 0
18750 / 16 = 1171, remains 14 or E
1171 / 16 = 73, remains 3
73 / 16 = 4, remains 9
4 / 16 = 0, remains 4
300000 decimal number equal to 493E0 hexadecimal number
300000 ₍₁₀₎ = 493E0 ₍₁₆₎

Read more »»

Decimal numbers to octal numbers

Convert decimal numbers to octal numbers
1. 60
2. 133
3. 512

Completion:
1. 60 ₍₁₀₎ = ? ₍₈₎
→ 60 / 8 = 7, remains 4
→ 7 / 8 = 0, remains 7
* Finish when meet zero (0) and then write remains numbers, from bottom to top
60 decimal number equal to 74 octal number
60 ₍₁₀₎ = 74 ₍₈₎

2. 133 ₍₁₀₎ = ? ₍₈₎
133 / 8 = 16, remains 5
16 / 8 = 2, remains 0
2 / 8 = 0, remains 2
133 decimal number equal to 205 octal number
133 ₍₁₀₎ = 205 ₍₈₎

3. 512 ₍₁₀₎ = ? ₍₈₎
512 / 8 = 64, remains 0
64 / 8 = 8, remains 0
8 / 8 = 1, remains 0
1 / 8 = 0, remains 1
512 decimal number equal to 1000 octal number
512 ₍₁₀₎ = 1000 ₍₈₎

Read more »»

Decimal numbers to binary numbers

Convert decimal numbers to binary numbers
1. 10
2. 31
3. 42

Completion:
1. 10 ₍₁₀₎ = ? ₍₂₎
→ 10 / 2 = 5, remains 0
→ 5 / 2 = 2, remains 1
→ 2 / 2 = 1, remains 0
→ 1 / 2 = 0, remains 1
* Finish when meet zero (0) and then write remains numbers, from bottom to top
10 decimal number equal to 1010 binary number
10 ₍₁₀₎ = 1010 ₍₂₎

2. 31 ₍₁₀₎ = ? ₍₂₎
31 / 2 = 15, remains 1
15 / 2 = 7, remains 1
7 / 2 = 3, remains 1
3 / 2 = 1, remains 1
1 / 2 = 0, remains 1
31 decimal number equal to 11111 binary number
31 ₍₁₀₎ = 11111 ₍₂₎

3. 42 ₍₁₀₎ = ? ₍₂₎
42 / 2 = 21, remains 0
21 / 2 = 10, remains 1
10 / 2 = 5, remains 0
5 / 2 = 2, remains 1
2 / 2 = 1, remains 0
1 / 2 = 0, remains 1
42 decimal number equal to 101010 binary number
42 ₍₁₀₎ = 101010 ₍₂₎

Read more »»

Table four number systems, comparison of 0 to 32 of each number

Table four number systems: decimal, binary, octal and hexa-decimal, which contain number 0 to 32 of each number, is made to make it easier when have an exercise of digital technique.

Here's is the table

Number system
Decimal	Binary	Octal	Hexa-decimal
0	0	0	0
1	1	1	1
2	10	2	2
3	11	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F
16	10000	20	10
17	10001	21	11
18	10010	22	12
19	10011	23	13
20	10100	24	14
21	10101	25	15
22	10110	26	16
23	10111	27	17
24	11000	30	18
25	11001	31	19
26	11010	32	1A
27	11011	33	1B
28	11100	34	1C
29	11101	35	1D
30	11110	36	1E
31	11111	37	1F
32	100000	40	20

Read more »»

Hexa decimal number

Hexa decimal number is system number who have 16 digit numbers, which is 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E and F, where:
A present of 10
B present of 11
C present of 12
D present of 13
E present of 14
F present of 15.
Hexa decimal number base 16 numeral system.

Hexa decimal number weights
16⁰ = 1 → first digit, weights one
16¹ = 16 → second digit, weights sixteen
16² = 256 → third digit, weights two hundred and six
16³ = 4096 → fourth digit, weights 512
16⁴ = 65536 → fifth digit, weights 4096
etc.

Example 1:
Convert Hexa decimal number 750 to decimal number

Completion:
750 ₍₁₆₎ = ? ₍₁₀₎
0 → 0 × 16⁰ = 0
5 → 5 × 16¹ = 80
7 → 7 × 16² = 7 × 256 = 1792
750 → 0 + 80 + 1792 = 1872
750 ₍₁₆₎ = 1872 ₍₁₀₎.

Example 2:
Convert Hexa decimal number 20BCA to decimal number

Completion:
20BCA ₍₁₆₎ = ? ₍₁₀₎
A → 10 × 16⁰ = 10
C → 12 × 16¹ = 192
B → 11 × 16² = 11 × 256 = 2816
0 → 0 × 16³ = 0
2 → 2 × 16⁴ = 2 × 65536 = 131072
20BCA → 10 + 192 + 2816 + 0 + 131072 = 134090
20BCA ₍₁₆₎ = 134090 ₍₁₀₎.

Read more »»

Octal number

Octal number is system number who have 8 digit numbers, which is 0, 1, 2, 3, 4, 5, 6 and 7. Octal number base 8 numeral system.

Octal number weights
8⁰ = 1 → first digit, weights one
8¹ = 8 → second digit, weights eight
8² = 64 → third digit, weights sixty four
8³ = 512 → fourth digit, weights 512
8⁴ = 4096 → fifth digit, weights 4096
etc.

Example 1:
Convert Octal number 370 to decimal number

Completion:
370 ₍₈₎ = ? ₍₁₀₎
0 → 0 × 8⁰ = 0
7 → 7 × 8¹ = 56
3 → 3 × 8² = 192
370 → 0 + 56 + 192 = 248
370 ₍₈₎ = 248 ₍₁₀₎

Example 2:
Convert Octal number 55017 to decimal number

Completion:
55017 ₍₈₎ = ? ₍₁₀₎
7 → 7 × 8⁰ = 7
1 → 1 × 8¹ = 8
0 → 0 × 8² = 0
5 → 5 × 8³ = 2560
5 → 5 × 8⁴ = 20480
55017 → 7 + 8 + 0 + 2560 + 20480 = 23055
55017 ₍₈₎ = 23055 ₍₁₀₎

Read more »»

Decimal number

Decimal number is system number who have 10 digit numbers, consist of 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9. Decimal number base 10 numeral system, and it's the most used in the system numbers.

Decimal number weights
10⁰ = 1 → first digit, weights one
10¹ = 10 → second digit, weights ten
10² = 100 → third digit, weights hundred
10³ = 1000 → fourth digit, weights thousand
10⁴ = 1000 → fifth digit, weights ten thousand
etc.

Example 1:
Describe a decimal number 2015 in the system numbers

Completion:
2015 ₍₁₀₎ =
5 → 5 × 10⁰ = 5
1 → 1 × 10¹ = 10
0 → 0 × 10² = 0
2 → 2 × 10³ = 2000
2015 → 5 + 10 + 0 + 2000 = 2015

Example 2:
Describe a decimal number 1000518 in the system numbers

Completion:
1000518 ₍₁₀₎ =
8 → 8 × 10⁰ = 8
1 → 1 × 10¹ = 10
5 → 5 × 10² = 500
0 → 0 × 10³ = 0
0 → 0 × 10⁴ = 0
0 → 0 × 10⁵ = 0
1 → 1 × 10⁶ = 1000000
1000518 → 8 + 10 + 500 + 0 + 0 + 0 + 1000000 = 1000518.

Read more »»

Binary number

Binary number is system number who have 2 digit numbers, which is 0 and 1. Binary number base 2 numeral system.

Binary number weights
2⁰ = 1 → first digit, weights one
2¹ = 2 → second digit, weights two
2² = 4 → third digit, weights four
2³ = 8 → fourth digit, weights eight
2⁴ = 16 → fifth digit, weights sixteen
etc.

Example 1:
Convert binary number 110 to decimal number

Completion:
110 ₍₂₎ = ? ₍₁₀₎
0 → 0 × 2⁰ = 0
1 → 1 × 2¹ = 2
1 → 1 × 2² = 4
110 → 0 + 2 + 4 = 6
110 ₍₂₎ = 6 ₍₁₀₎

Example 2:
Convert binary number 11010 to decimal number

Completion:
11010 ₍₂₎ = ? ₍₁₀₎
0 → 0 × 2⁰ = 0
1 → 1 × 2¹ = 2
0 → 0 × 2² = 0
1 → 1 × 2³ = 8
1 → 1 × 2⁴ = 16
11010 → 0 + 2 + 0 + 8 + 16 = 26
11010 ₍₂₎ = 26 ₍₁₀₎

Read more »»

Number system in electronics digital techniques

Number system in Electronics Digital Techniques, is divided into four types, namely:
1. Binary numbers,
for example: 10 ₍₂₎ --> 2 digit, 111 ₍₂₎ --> 3 digit, 1001 ₍₂₎ --> 4 digit, 1101010 ₍₂₎ --> more digit

2. Decimal numbers,
for example: 19 ₍₁₀₎ --> 2 digit, 501 ₍₁₀₎ --> 3 digit, 8081₍₁₀₎ --> 4 digit, 87259000₍₁₀₎ --> more digit

3. Octal numbers,
for example: 17 ₍₈₎ --> 2 digit, 645 ₍₈₎ --> 3 digit, 2571 ₍₈₎ --> 4 digit, 7257001 ₍₈₎ --> more digit

4. Hexa-decimal numbers,
for example: 1A ₍₁₆₎ --> 2 digit, 2E1 ₍₁₆₎ --> 3 digit, AB212 ₍₁₆₎ --> 4 digit, 31FB9012 ₍₁₆₎ --> more digit

The numbers are in parentheses, indicate the type of numbers. This numbering system can be converted or transformed, from one number system to another number system.

Read more »»