Kirchoff's current law
KCL (Kirchoff's Current Law) reads:
Written by equation
Σ I = 0
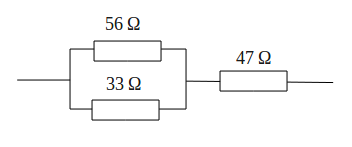
See electric current branching scheme as in the circuit below

Currents toward to the point A marked as positive (+), the points are IA, IB and ID.
Currents out of the point A marked as negative (-), that is IC
The equation becomes:
IA + IB - IC + ID = 0
IA + IB + ID = IC
Example question:
In the circuit above, it is known that IA = 10 A, IB = 6 A, IC = 18 A. What ID current is given to the circuit?
completion:
IA + IB - IC + ID = 0
10 + 6-18 + ID = 0
ID = 18 - 16 = 2 A
Algebraic sum of electric currents flowing toward to a point or a branching of a circuit, equal to the current that out of the point.
Written by equation
Σ I = 0
See electric current branching scheme as in the circuit below

Currents toward to the point A marked as positive (+), the points are IA, IB and ID.
Currents out of the point A marked as negative (-), that is IC
The equation becomes:
IA + IB - IC + ID = 0
IA + IB + ID = IC
Example question:
In the circuit above, it is known that IA = 10 A, IB = 6 A, IC = 18 A. What ID current is given to the circuit?
completion:
IA + IB - IC + ID = 0
10 + 6-18 + ID = 0
ID = 18 - 16 = 2 A









 Less than half a year has a netbook, optical mouse has been damaged. Damage that occurs, the red indicator light is on but the mouse cursor was quiet, the pointer does not move following the mouse movements.
Less than half a year has a netbook, optical mouse has been damaged. Damage that occurs, the red indicator light is on but the mouse cursor was quiet, the pointer does not move following the mouse movements.