Capacitor and capacitance of capacitor
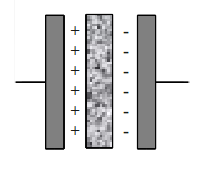
A capacitor consists of two sides of a metal plate with an insulating layer (partition) located between these two plates. Insulator layer that is used can be a thin plastic plate, but in some types of capacitors, this layer is air.

Picture above shows examples of the capacitor and picture below is a symbol of the capacitor.

If a capacitor is connected to a DC source, the electrons will gather at the plate that is connected to the negative terminal of the source. These electrons will reject electrons that exist on the opposite plate. Electrons are rejected will flow towards the positive terminal of the source.

A capacitor is connected like this to the source, will be charged immediately. Voltages between the two plates is equal to the voltage power source. When the capacitor is released from the source, the capacitor retains the charge. Due to insulator layer on the capacitor, the current can not flow through the capacitor. Capacitor will remain charged up to infinite time. For this reason, capacitors are very useful for keep electrical charge.
Capacitance
The ability of a capacitor to keep electrical charge is called capacitance of capacitor, with the symbol C. Unit for capacitance is farad, which is symbolized by F. One farad is defined as the amount of electrical charge that can be saved (in units of coulombs) by unit of voltage.
Capacitance of capacitor = electrical charge / voltage
Example:
Electrical charge keep in a capacitor is 6 coulombs. Voltages between the two plates is 2 V. What is the value of capacitance?
Completion:
Capacitance of capacitor = 6 / 2 = 3 F
Capacitor values
Capacitors made with a value similar to the reference values for the resistor. Capacitors have a higher tolerance than the resistor, so that we do not find it necessary to create as much as 24 pieces of value within that range. Capacitance values in this range are:
1,0 1,2 1,5 1,8 2,2 2,7 3,3 3,9 4,7 5,6 6,8 8,2
These values are repeated again with a multiple of 10.

Picture above shows examples of the capacitor and picture below is a symbol of the capacitor.

If a capacitor is connected to a DC source, the electrons will gather at the plate that is connected to the negative terminal of the source. These electrons will reject electrons that exist on the opposite plate. Electrons are rejected will flow towards the positive terminal of the source.

A capacitor is connected like this to the source, will be charged immediately. Voltages between the two plates is equal to the voltage power source. When the capacitor is released from the source, the capacitor retains the charge. Due to insulator layer on the capacitor, the current can not flow through the capacitor. Capacitor will remain charged up to infinite time. For this reason, capacitors are very useful for keep electrical charge.

Capacitance
The ability of a capacitor to keep electrical charge is called capacitance of capacitor, with the symbol C. Unit for capacitance is farad, which is symbolized by F. One farad is defined as the amount of electrical charge that can be saved (in units of coulombs) by unit of voltage.
Capacitance of capacitor = electrical charge / voltage
Example:
Electrical charge keep in a capacitor is 6 coulombs. Voltages between the two plates is 2 V. What is the value of capacitance?
Completion:
Capacitance of capacitor = 6 / 2 = 3 F
Capacitor values
Capacitors made with a value similar to the reference values for the resistor. Capacitors have a higher tolerance than the resistor, so that we do not find it necessary to create as much as 24 pieces of value within that range. Capacitance values in this range are:
1,0 1,2 1,5 1,8 2,2 2,7 3,3 3,9 4,7 5,6 6,8 8,2
These values are repeated again with a multiple of 10.







No comments
No spam, no active link, please ^_^